What is activation checkpointing?
Activation checkpointing is a technique used to save GPU memory while training large deep learning models. During the training of a deep learning model, we store the activations in memory to calculate the gradients during the backward pass. Activation checkpointing literally skips the saving part, thus saving a lot of memory. The figure below will give you an idea of the huge amount of memory consumed by activations while training a model:
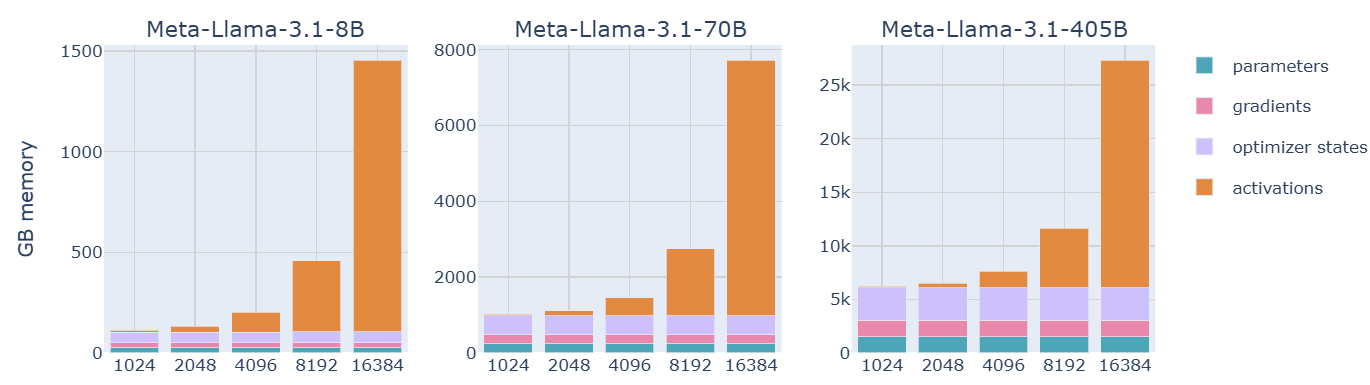 Source: The Ultra-Scale Playbook -
Training LLMs on GPU Clusters
Source: The Ultra-Scale Playbook -
Training LLMs on GPU Clusters
So instead of storing activations in memory, we re-calculate those activations during the backward pass. Thus, we essentially save a lot of memory at the cost of slightly more computation. Mostly we do selective activation checkpointing. This means we skip the storing of activations for some layers while keeping the rest of the activations in memory.
How are activations used in the backward pass?
Here is a simple example of what we actually mean by activations and how they are used in the backward pass:
-
Consider a 3 layer neural network with $f_1$, $f_2$ and $f_3$ representing the transformation applied on each layer respectively.
-
Consider the input $x$, we get the final output of the neural network $y$ by literally doing this:
$$ a_1 = f_1(x) $$ $$ a_2 = f_2(a_1) $$ $$ y = f_3(a_2 )$$
where $a_1$, $a_2$ and $y$ are the activations of each layer.
-
Assume that the loss $L$ is calculated as follows:
$$ L = (y - y_{true})^2 $$
where $y_{true}$ is the ground truth.
-
To update the weights during the gradient descent step, we need to calculate the gradients for each layer using the chain rule. Let’s represent the gradients of each layer by $g_1$, $g_2$ and $g_3$ respectively. Here is a break down of the steps involved in the calculation of gradients for each layer:
$$ g_3 = \frac{\partial L}{\partial a_2} = \frac{\partial L}{\partial y} \cdot \frac{\partial y}{\partial a_2} $$
$$ g_2 = \frac{\partial L}{\partial a_1} = \frac{\partial L}{\partial y} \cdot \frac{\partial y}{\partial a_2} \cdot \frac{\partial a_2}{\partial a_1} = g_3 \cdot \frac{\partial a_2}{\partial a_1} $$
$$ g_1 = \frac{\partial L}{\partial x} = \frac{\partial L}{\partial y} \cdot \frac{\partial y}{\partial a_2} \cdot \frac{\partial a_2}{\partial a_1} \cdot \frac{\partial a_1}{\partial x} = g_2 \cdot \frac{\partial a_1}{\partial x} $$
To calculate the gradient for a layer, we need the inputs and activations of that layer and the gradients of all the future layers. This is how we implement the above equations in code:
import torch
### Function transformation for each layer
# f₁, f₂ and f₃
def f1(x): return x ** 2
def f2(x): return x ** 3
def f3(x): return x ** 4
# set `y_true=10` for now
def loss(y, y_true=10): return (y - y_true) ** 2
### Derivatives of each function transformation
def df1(x): return 2 * x # ∂L/∂x
def df2(x): return 3 * (x ** 2) # ∂L/∂a₁
def df3(x): return 4 * (x ** 3) # ∂L/∂a₂
def dloss(y, y_true=10): return 2 * (y - y_true) # ∂L/∂y
### Calculate the activations -> forward pass
x = torch.tensor(5., requires_grad=True)
a1 = f1(x) # x → f₁ → a₁
a2 = f2(a1) # a₁ → f₂ → a₂
y = f3(a2) # a₂ → f₃ → y
l = loss(y)
### Calculate the gradients -> backward pass
# ∂L/∂a₂ = (∂L/∂y).(∂y/∂a₂)
g3 = dloss(y) * df3(a2)
# ∂L/∂a₁ = g₃.(∂a₂/∂a₁)
g2 = g3 * df2(a1)
# ∂L/∂x = g₂.(∂a1/∂x)
g1 = g2 * df1(x)
You can compare the value of g1 with that of torch as follows:
# calculate `∂L/∂x` using torch
torch_grad, = torch.autograd.grad(l, x)
# check if the gradients are equal
torch.allclose(torch_grad, g1)
## Output: `True`
Activation checkpointing in action
PyTorch’s built-in activation checkpointing
So the action plan here is to create a simple neural network and apply torch.utils.checkpoint to some layers in the model (selective activation checkpointing). We then compare the GPU memory with and without the activation checkpoint.
The neural network architecture (create utils.py file and save the below code):
from torch import nn
from torch.utils import checkpoint
class MLP(nn.Module):
def __init__(self, use_checkpoint=False):
super().__init__()
# whether to apply activation checkpointing
self.use_checkpoint = use_checkpoint
# X => block_1 -> block_2 -> block_3 => y
self.block_1 = nn.Sequential(
nn.Linear(3000, 512),
nn.ReLU(),
nn.Linear(512, 700),
)
self.block_2 = nn.Sequential(
nn.Linear(700, 512),
nn.ReLU(),
nn.Linear(512, 700),
)
self.block_3 = nn.Sequential(
nn.Linear(700, 512),
nn.ReLU(),
nn.Linear(512, 10),
)
def forward(self, x):
if self.use_checkpoint:
# activations are not stored in memory for layers inside
# `_checkpoint_layers` method, we recomputes it in the backward pass
out = checkpoint.checkpoint(self._checkpoint_layers, x)
else:
out = self._checkpoint_layers(x)
out = self.block_3(out)
return out
def _checkpoint_layers(self, x):
return self.block_2(self.block_1(x))
For benchmarking the memory consumption, we will define a simple utility function get_mem_consumption (save this in utils.py). The function takes the model and passes in a random input and calculates the peak memory consumption in the GPU during the forward pass:
import torch
def get_mem_consumption(model, device):
# reset stats
torch.cuda.reset_peak_memory_stats(device)
# forward pass
x = torch.randn(1024*3, 3000, device=device, requires_grad=True)
out = model(x)
# max memory consumption (in MB)
max_mem = torch.cuda.max_memory_allocated(device) / 1e+6
# backward pass
out.backward(torch.ones_like(out))
return max_mem
Let’s also write a function (also saved in utils.py) to ease out the benchmarking process:
def run_benchmark(use_checkpoint):
device = "cuda"
# get the model
model = MLP(use_checkpoint=use_checkpoint).to(device)
# forward & backward pass, return memory consumption
mem_consumption = get_mem_consumption(model, device)
print(f"Memory consumption with `use_checkpoint={use_checkpoint}`: {mem_consumption:.2f} MB")
We can simply call run_benchmark with use_checkpoint=True and use_checkpoint=False from the same script, but I found some discrepancies in the reported memory consumption while doing so. So I prefer to run them separately.
- GPU memory consumption without activation checkpointing:
from utils import run_benchmark
run_benchmark(use_checkpoint=False)
## Output - Memory consumption with `use_checkpoint=False`: 101.04 MB
- GPU memory consumption with activation checkpointing:
from utils import run_benchmark
run_benchmark(use_checkpoint=True)
## Output - Memory consumption with `use_checkpoint=True`: 83.21 MB
Verify activation checkpointing with PyTorch hooks
If you are like me, you might want to know if the activations are really getting stored in memory or not. We will write a simple PyTorch hook to verify this (saved in utils.py). We will apply this hook to each layer during the forward pass of the model.
def register_forward_hooks(model):
# function called during the forward pass
def forward_hook(module, inp, out):
# for layers where `requires_grad=False`, the activations are
# re-computed during the backward pass
print(f"Forward pass for `{module.__class__.__name__}`: Activations stored = {out.requires_grad}")
# register forward hook for each layer in the model
for name, layer in model.named_modules():
if isinstance(layer, nn.Sequential):
for i in range(len(layer)):
layer[i].register_forward_hook(forward_hook)
Now we have to slightly modify run_benchmark function to incorporate this hook in the model before doing the forward pass:
def run_benchmark(use_checkpoint, verify=False):
device = "cuda"
# get the model
model = MLP(use_checkpoint=use_checkpoint).to(device)
if verify:
# register hook
register_forward_hooks(model)
# forward & backward pass, return memory consumption
mem_consumption = get_mem_consumption(model, device)
print(f"Memory consumption with `use_checkpoint={use_checkpoint}`: {mem_consumption:.2f} MB")
The output of running run_benchmark(use_checkpoint=True, verify=True) is as follows:
Forward pass for `Linear`: Activations stored = False
Forward pass for `ReLU`: Activations stored = False
Forward pass for `Linear`: Activations stored = False
Forward pass for `Linear`: Activations stored = False
Forward pass for `ReLU`: Activations stored = False
Forward pass for `Linear`: Activations stored = False
Forward pass for `Linear`: Activations stored = True
Forward pass for `ReLU`: Activations stored = True
Forward pass for `Linear`: Activations stored = True
Forward pass for `Linear`: Activations stored = True
Forward pass for `ReLU`: Activations stored = True
Forward pass for `Linear`: Activations stored = True
Forward pass for `Linear`: Activations stored = True
Forward pass for `ReLU`: Activations stored = True
Forward pass for `Linear`: Activations stored = True
As expected, the activations for layers in the first two blocks of our neural network are not stored in memory during the forward pass.
Implement your own activation checkpointing
Finally, we are ready to implement our activation checkpointing class that we could use instead of torch.utils.checkpoint (implemented in utils.py). Here, sub-classing from torch.autograd.Function makes our lives easier. We could simply define the logic for modifying the normal behavior of forward and backward pass under forward and backward methods (pytorch team has a good documentation here if you are interested):
class CustomCheckpointFunction(torch.autograd.Function):
@staticmethod
def forward(ctx, func, inputs):
# save the inputs & function transformation for backward pass
# `func` would be the `_checkpoint_layers` defined in our model
ctx.save_for_backward(inputs)
ctx.func = func
# return the output of the layer
with torch.no_grad():
return func(inputs)
@staticmethod
def backward(ctx, grad_outputs):
# get the inputs saved from forward pass
inputs, = ctx.saved_tensors
# re-compute the activation for the layer
# using the function transformation saved from forward pass
with torch.enable_grad():
outputs = ctx.func(inputs)
# compute the gradients for the layer
return (None, *torch.autograd.grad(outputs, inputs, grad_outputs))
In the final step of backward method, doing torch.autograd.grad(outputs, inputs, grad_outputs) is the same as $g_2 \cdot \frac{\partial a_1}{\partial x}$ and $g_3 \cdot \frac{\partial a_2}{\partial a_1}$ in mathematical sense. We multiply the gradients of future layers with gradient of the current layer (we’ve discussed this earlier in the post).
We could simply replace torch.utils.checkpoint with our custom checkpoint function and it would work exactly the same. So our model definition would look like this, just a slight change in the forward method:
class MLP(nn.Module):
def __init__(self, use_checkpoint=False):
...
def forward(self, x):
if self.use_checkpoint:
# replace with our custom checkpoint function
# func -> `self._checkpoint_layers`
# inputs -> `x`
out = CustomCheckpointFunction.apply(self._checkpoint_layers, x)
else:
out = self._checkpoint_layers(x)
out = self.block_3(out)
return out
def _checkpoint_layers(self, x):
...
Whoa, that’s a whole lot for a quick explainer :) Started from the theory, all the way to understanding gradient computation to implementing pytorch hooks to verify the checkpointing and finally implementing our own activation checkpointing using PyTorch’s autograd function. That would wrap up this quick explainer.
You can access the complete code used in this post here.
References
[1] “The Ultra-Scale Playbook - a Hugging Face Space by Nanotron.”. Huggingface.co. 2025.
[2] “PyTorch: Defining New Autograd Functions — PyTorch Tutorials 2.6.0+Cu124 Documentation”. Pytorch.org. 2024.
[3] “PyTorch 101: Understanding Hooks | DigitalOcean.”. Digitalocean.com. 2025.